Distribusi Normal: Pengertian, Ciri-Ciri dan Contoh Soal

Di dalam ilmu atau pembahasan statistika, tentu sudah tidak asing dengan istilah distribusi normal. Hal tersebut sangat berkaitan dengan distribusi peluang atau distribusi probabilitas. Distribusi normal adalah fungsi probabilitas yang menunjukkan adanya distribusi (penyebaran) suatu variabel. Berikut pengertian distribusi normal, kurva dan contoh.

Istilah distribusi normal tersebut kerap digunakan sebagai bahan perhitungan akan berbagai fenomena dalam kehidupan sehari-hari.

Biasanya, digunakan sebagai perhitungan tinggi badan, perhitungan kesalahan, tekanan darah, hingga penjabaran nilai IQ. Sehingga istilah distribusi normal memiliki fungsi menjadi densitas. Istilah distribusi normal juga disebut sebagai distribusi Gauss. Namun, apa itu pengertian distribusi normal dan berbagai hal mengenai distribusi normal?

Di bawah ini akan dijelaskan secara mendalam dan lebih jelas mengenai apa itu distribusi normal, bagaimana ciri-ciri distribusi normal, apa saja syarat distribusi normal, parameter dari distribusi normal, hingga berbagai contoh distribusi normal.

Apa Itu Distribusi Normal?

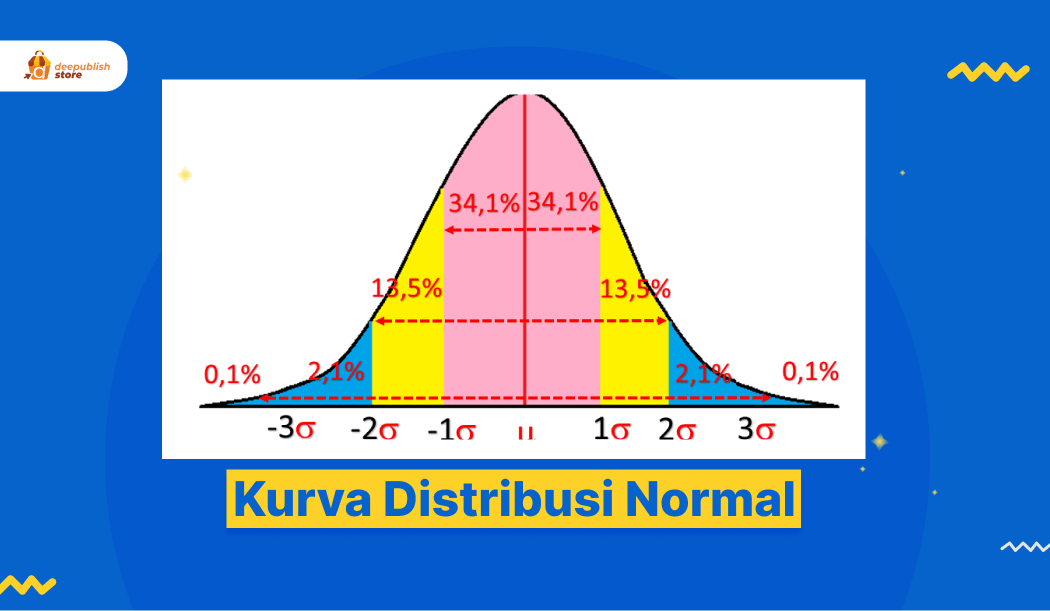
Distribusi normal merupakan fungsi probabilitas yang menunjukkan adanya distribusi atau penyebaran suatu variabel. Fungsi dari distribusi normal tersebut biasanya dibuktikan oleh adanya grafik simetris yang disebut kurva lonceng atau bell curve yang menandakan adanya distribusi yang merata, sehingga kurva akan memuncak di bagian tengah dan melandai di kedua sisi dengan nilai yang setara.

Distribusi normal juga dapat diartikan sebagai salah satu jenis distribusi variabel acak kontinu yang berbentuk lonceng atau grafik. Distribusi normal ini dibuat dengan fungsi probabilitas yang kemudian digunakan untuk menunjukkan variasi atau penyebaran distribusi, sehingga fungsi yang nantinya akan dibuktikan dengan menggunakan suatu grafik simetris atau bell curve.

Istilah distribusi normal atau yang juga disebut Gauss mengacu kepada Carl Friedrich Gauss yakni seorang Matematikawan Jerman yang mengembangkan sebuah teori distribusi dengan fungsi eksponensial dengan dua parameter periode 1794-1809.

Dengan adanya distribusi tersebut, berpusat pada simetris pada nilai rata-rata seluruh data dalam suatu populasi sehingga penilaian berat sebelah atau tidak seimbang kemudian dapat dihindarkan. Hal ini dapat membantu dalam penentuan tingkat normalitas serta terjadinya kecenderungan sentral yang merupakan hal penting dan tidak boleh diabaikan begitu saja.

Ketika penggunaan distribusi normal ini digunakan, maka tingkat normalitas data atau kecenderungan sentral bisa ditentukan dengan lebih mudah untuk dilakukan. Sehingga penerapannya mampu meningkatkan objektivitas penilaian sehingga hal ini membantu dalam menempatkan para anggota dengan tepat, khususnya dalam suatu kelompok.

Dalam satu kriteria yang sama, distribusi normal digunakan untuk menghindari terjadinya penilaian yang condong atau biasa di satu kategori saja, sehingga dengan distribusi yang terpusat dan simetris pada nilai rata-rata seluruh data pada suatu populasi, penilaian yang berat sebelah atau tidak seimbang kemudian akan dapat dihindarkan.

Penerapan teori distribusi normal ini dianggap penting karena adanya beberapa alasan. Mulai dari meningkatkan objektivitas penilaian sehingga kemudian dapat membantu menempatkan anggota yang paling tepat untuk suatu kelompok tertentu sehingga dapat melakukan evaluasi nilai atau terjadinya pengelompokkan pegawai dalam satu kriteria yang sama.

Sehingga tujuan atau parameter diterapkannya distribusi normal menghindari adanya bias atau penilaian yang condong pada satu kategori saja. Distribusi normal juga dapat membantu menentukan tingkat normalitas yang cenderung pada sentrial. Misalnya pada statistika peluang, normalitas suatu data merupakan hal penting yang anti-untuk diabaikan.

Dengan demikian, artinya semakin kecil nilai deviasi, maka kurva akan berbentuk semakin runcing. Selain itu, terjadinya standar deviasi juga menggambarkan jarak atau selisih umum antara nilai rata-rata atau mean dengan data lain yang diobservasi.

Baca Juga: Metode Eksperimen

Ciri-Ciri Distribusi Normal

Untuk membedakan distribusi normal dengan distribusi lain di dalam statistika, tentu ada karakteristik atau ciri-ciri yang membedakan. Berikut merupakan ciri-ciri distribusi normal yang membedakan distribusi normal dengan distribusi jenis lainnya.

1. Teori distribusi memiliki nilai mean, median, dan juga modus yang sama. Oleh karena itu distribusinya sering disebut dengan unimodal. Kurva distribusi bisa bersifat simetris dengan bentuk lonceng atau bell curve.
2. Titik puncak kurva pada nilai rata-rata, nilai ini berada di posisi tengah kurva. Kemudian pada data distribusi terletak pada sekitar garis lurus yang ditarik ke bawah yang berasal dari titik tengah.
3. Nilai rata-rata atau mean merupakan nilai dengan standar deviasi untuk menentukan lokasi dan juga bentuk distribusi tersendiri.
4. Jumlah luas daerah yang terletak di bawah kurva normal memiliki nilai 1. Di antaranya adalah setengah (1/2) pada sisi kanan dan juga setengah (1/2) pada sisi kiri. Hal ini juga berlaku ke seluruh distribusi probabilitas kontinyu.
5. Kurva distribusi disimpulkan jika setengah dari data populasi kemudian memiliki nilai yang kurang dari angka rata-rata. Sementara bagian yang lain lagi punya nilai yang jauh lebih besar.
6. Masing-masing ekor kurva pada kedua sisi kemudian dapat memanjang dengan tak terbatas. Di berbagai kasus perhitungan distribusi, ekor kurva bahkan dapat memotong sumbu horizontal.

Syarat Distribusi Normal

Untuk menerapkan distribusi normal, tentu ada syarat atau aturan yang berlaku. Perlu diketahui, deviasi standar sangat berharga di dalam data yang terdistribusi secara normal. Sehingga deviasi standar juga dapat digunakan untuk menentukan proporsi nilai yang mana termasuk ke dalam sejumlah deviasi standar tertentu dari rata-rata.

Di dalam distribusi normal sebanyak 68% terdapat pengamatan dalam kisaran +/-1 standar deviasi dari rata-rata. Pada 95% dalam kisaran +/-2 standar deviasi, dan 99,7% dalam kisaran +/-3 dari rata-rata.

Penilaian atau properti tersebut merupakan bagian dari aturan empiris. Aturan empiris tersebut digunakan untuk menjelaskan adanya persentase data yang termasuk di dalam jumlah tertentu pada deviasi standar dari nilai rata-rata atau mean untuk kurva berbentuk lonceng.

Artikel Terkait: Fokus Penelitian Adalah

Parameter dari Distribusi Normal

Penerapan distribusi normal ini dianggap penting karena terdapat beberapa alasan. Mulai dari adanya meningkatkan objektivitas penilaian, kemudian membantu menempatkan anggota yang paling tepat untuk suatu kelompok tertentu untuk melakukan evaluasi nilai atau dilakukannya pengelompokan pegawai di dalam satu kriteria yang sama.

Tujuan dilakukannya adalah untuk menghindari adanya bias atau penilaian yang condong pada satu kategori saja. Sehingga tak heran jika distribusi simetris dan berpusat pada nilai rata-rata secara keseluruhan populasi dengan penilaian yang berat sebelah tidak bisa dihindarkan.

Distribusi normal juga mampu membantu menentukan tingkat normalitas yang cenderung sentral sehingga pada statistika peluang, normalitas suatu data menjadi hal penting yang tidak bisa diabaikan.

Dengan adanya distribusi simetris, maka akan membantu menentukan tingkat normalitas dengan kecenderungan sentral. Di dalam statistika, khususnya statistika peluang, sehingga normalitas suatu data merupakan hal penting yang tidak boleh diabaikan.

Teori distribusi Gauss ini memiliki kecenderungan sentral atau tingkat normalitas data juga dapat ditentukan secara lebih mudah, sehingga dengan demikian informasi mengenai distribusi normal serta adanya parameter dan karakteristik yang melengkapi penerapannya.

Bagi yang sedang mempelajari statistika peluang atau sedang mencari teori pendukung di dalam penghitungan data, maka informasi di atas dapat dijadikan sebagai salah satu referensi. Misalnya pada teori distribusi lain di dalam statistika, bentuk kurva nilai peluang distribusi normal ditentukan oleh sejumlah parameter.

Perlu diketahui, teori distribus lain statistika probabilitas, berbentuk kurva, nilai peluang tabel distribusi normal ditentukan dalam sejumlah parameter. Seperti halnya teori distribusi yang lain di dalam statistika, distribusi ini juga dibagi menjadi beberapa jenis parameter yang dijadikan acuan, yaitu mean atau nilai rata-rata serta standar deviasi atau simpangan baku.

1. Digunakan sebagai Pusat Distribusi

Nilai rata-rata atau mean digunakan sebagai pusat distribusi atau penyebaran nilai lainnya. Sehingga nilai tersebut akan menentukan lokasi titik puncak dalam kurva lonceng, sedangkan nilai-nilai lainnya akan menyebar mengikuti rerata.

2. Perhitungan Variabilitas

Standar deviasi merupakan perhitungan variabilitas yang menentukan lebar sebuah kurva distribusi normal. Dengan demikian, maka standar ini dapat digunakan untuk menghitung seberapa jauh adanya kecenderungan data yang akan melebar dari nilai rata-rata yang menjadi titik pusatnya.

3. Melawan Perkiraan Sampel

Parameter distribusi normal populasinya melawan perkiraan sampel. Artinya, rata-rata dan deviasi standar menjadi nilai parameter yang berlaku di dalam seluruh populasi. Sehingga di dalam suatu distribusi normal, ahli statistik akan memberi penanda parameter yang menggunakan simbol Yunani μ (mu) untuk mean populasi dan juga simbol σ (sigma) untuk penerapan deviasi standar populasi.

Secara umum, parameter populasi umumnya tidak diketahui karena tidak memungkinkan suatu pengukuran terhadap seluruh populasi. Pada data sampel secara acak yang digunakan untuk menghitung estimasi parameter.
Dalam sampel yang acak untuk menghitung estimasi parameter juga bisa digunakan, ahli statistik menggunakan estimasi sampel dari parameter dengan menggunakan simbol x̅ untuk mean sampel dan juga s untuk deviasi standar sampel.

Contoh Distribusi Normal

Untuk mengetahui lebih lanjut bagaimana distribusi normal, berikut disajikan contoh distribusi normal agar Anda lebih memahami mengenai distribusi normal.

Perlu diketahui lebih dahulu, ciri-ciri distribusi normal berbentuk lonceng simetris terhadap   x = μ distribusi normal atau kurva normal disebut juga dengan nama distribusi Gauss, karena persamaan matematisnya ditemukan oleh Gauss dengan rumus sebagai berikut.

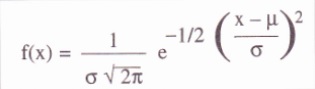
Di mana:

π = nilai konstan, yaitu 3,1416

c = nilai konstan, yaitu 2,7183

μ = parameter yang merupakan rata-rata distribusi

σ = parameter yang merupakan simpangan baku distribusi

Jika x mempunyai bentuk ∞ < x < ∞ maka disebut variabel acak x berdistribusi normal. Dan rumus di atas dapat digambarkan sebagai berikut:

Berikut contoh soal distribusi normal

Dari 100 responden didapat harga rata-rata untuk angket motivasi kerja = 75 dengan simpangan baku = 4

Ditanyakan:

1. Berapa jumlah responden yang mendapat nilai 80 ke atas?

2. Berapa nilai responden yang dapat dikualifikasikan 10 % dari nilai tertinggi?

Jawab:

1. Z = (80 – 75)/4

      = 1,25 dari tabel kurva normal didapat luas ke kanan = 10,56%.

Jadi jumlah responden = 10,56% x 100 = 11 orang

2. Batas kualifikasi 10% tertinggi = 50% – 10% = 40% dari tabel diperoleh 1,28. karena SD tertinggi 4, maka untuk 1,28SD = 1,28 x 4 = 5,12. jadi skor tertinggi = 75 + 5,12 = 80,12